الگوریتم پیج رنک (PageRank Algorithm) چیست؟ نحوه محاسبه و تاثیر در سئو سایت

عناوین مطالب
Toggleالگوریتم PageRank یک الگوریتم رتبه بندی صفحه است که توسط لری پیج و سرگئی برین، بنیانگذاران گوگل، توسعه داده شد. این الگوریتم بر اساس فرضیه ای کار می کند که صفحاتی که از صفحات معتبرتر لینک می گیرند، خود نیز معتبرتر هستند.
الگوریتم پیج رنک با محاسبه یک امتیاز برای هر صفحه وب کار می کند. این امتیاز با توجه به تعداد و کیفیت بک لینک های یک صفحه وب محاسبه می شود و از یک فرآیند ریاضی به نام زنجیره مارکوف برای محاسبه امتیاز PageRank استفاده می کند.
امروزه بیشتر در زمینه های مختلف استفاده می شود، به عنوان مثال در رتبه بندی کاربران در رسانه های اجتماعی و غیره… چیزی که در الگوریتم PageRank جذاب است این است که چگونه از یک مسئله پیچیده شروع کنیم و به یک راه حل بسیار ساده برسیم.
در این پست ایده و تئوری پیج رنک، یک الگوریتم گوگل را به شما آموزش می دهیم. شما فقط باید اصولی در جبر و زنجیره مارکوف داشته باشید. در اینجا، ما از رتبه بندی صفحات وب به عنوان یک مورد استفاده برای نشان دادن الگوریتم PageRank استفاده خواهیم کرد.
الگوریتم پیج رنک چیست؟
الگوریتم PageRank یکی از اولین الگوریتم های رتبه بندی صفحه بود که توسط موتورهای جستجو استفاده شد. این الگوریتم هنوز هم یکی از عوامل مهمی است که گوگل برای رتبه بندی صفحات وب در نتایج جستجو استفاده می کند.
برخی از مواردی که باید در مورد الگوریتم پیج رنک بدانید، در زیر آمده است:
- محاسبه پیج رنک برای صفحات هر وبسایت توسط گوگل با استفاده از فرمول های ریاضی بسیار پیچیده
- آپدیت شدن الگوریتم page rank در مدت زمان 3 الی 6 ماهه
- تاثیر زیاد بک لینک ها و کیفیت آن ها در بالا رفتن پیج رنک یک صفحه
- مقایسه شدن سایت با سایت های رقیب(سایت هایی که در حال استفاده از محتوا و کلمات کلیدی مشابه با سایت شما هستند) در روند بررسی الگوریتم پیج رنک
موارد زیادی می توانند در بالا رفتن رتبه توسط پیج رنک، تاثرگذار باشند. اول از همه باید بدانید که گوگل همواره 2 فاکتور اصلی ارتباط و اعتبار را برای رتبه دادن به سایت در نظر می گیرد؛ به این معنی که باید به موتور جستجو بفهمانید که محتوای صفحه شما در مورد چیست و این کار را با توجه به نکات بسیار زیاد و جزئی می توانید متوجه شوید. مورد دوم هم زمانی است که محتوای شما اطلاعات کافی را در مورد کلمه کلیدی مرتبط در اختیار کاربر قرار می دهد. به این ترتیب می توانید تا حد زیادی مطمئن باشید که محتوای شما می تواند رتبه خوبی دریافت کند.
اما در ادامه موارد دیگری نیز تاثیر دارد در اینکه شما را به لینک 1 تا 3 گوگل منتقل کنند. مورد اول در این لیست بک لینک است. الگوریتم پیج رنک زمانی که برنامه نویسی شد، موتورهای جستجوی دیگر(رقبای قدیمی گوگل) فقط محتوای داخل هر صفحه را بررسی می کردند و کاری به اتفاقات خارج سایت نداشتند. پیج رنک این روند را تغییر داد و این اولین دلیل تمایز عمیق گوگل با دیگر موتورهای جستجو بود.
الگوریتم Page Rank در وهله اول به تعداد بک لینک هایی که یک دامنه یا زیردامنه دریافت کرده، توجه می کرد. در ادامه به سراغ کیفیت آن بک لینک ها می رفت. در این روند 2 فاکتور مدنظر قرار می گرفت:
- تعداد بک لینک هایی که سایت یا صفحه شما دریافت کرده است.
- کیفیت سایت هایی که به سایت یا صفحه شما لینک داده اند.
هر چه درصد موارد بالا، بیشتر باشد، صفحه شما رتبه بهتری دریافت خواهد کرد.
پیج رنک می گوید: “صفحه ای که از این سایت های معتبر لینک دریافت کرده است، حتما دارای محتوای جامع، عالی و یونیکی است”.
فرآیند رتبه دهی الگوریتم پیج رنک به این صورت کار می کند:
- به هر صفحه وب در وب امتیازی اولیه داده می شود.
- سپس، امتیاز هر صفحه وب با توجه به امتیاز صفحاتی که به آن لینک می دهند، به روز می شود.
- این فرآیند تا زمانی ادامه می یابد که امتیازها به ثبات برسند.
همانطور که گفتیم، پیج رنک با استفاده از فرمول های سخت و پیچیده ای محاسبه می شود. روند این محاسبه را در ادامه می توانید بخوانید.
1. محاسبه رتبه صفحه با الگوریتم پیج رنک
رتبه صفحه با توزیع وزن در صفحات با هدف “به نظم در آوردن وب” بود. آنها این الگوریتم را بر اساس ایده یک وبگرد تصادفی در اینترنت ساخته اند که از یک صفحه بازدید می کند و با کلیک روی پیوندها به صفحات دیگر می رسد.
احتمال اینکه یک مرورگر تصادفی به یک صفحه خاص برسد، رتبه آن صفحه را مشخص می کند. امتیاز بر اساس یک مقیاس لگاریتمی بین 0 تا 10 محاسبه می شود که در آن 10 نشان دهنده قابل اعتمادترین منبع وب است که می تواند وجود داشته باشد.
رتبه صفحه یک معیار عینی است که با اهداف ذهنی جستجوگران همسو می شود: هرچه منابع بیشتری به یک صفحه اشاره کنند، اطلاعات موجود در آن صفحه ارزشمندتر است و کاربران احتمال بیشتری برای بازدید از آن دارند.
اما منابع ارجاع دهنده برابر نیستند، تعداد صفحاتی که به آنها پیوند می دهند نیز اندازه گیری می شود: هرچه یک صفحه ارجاع دهنده بک لینک بیشتری داشته باشد، قدرت PageRank در صفحه ای که به آن لینک می دهد بیشتر می شود.
فرمول اصلی PageRank در اینجا آمده است:
که در آن:
– A صفحه تحلیل شده است
– T1…Tn صفحاتی هستند که به صفحه تحلیل شده اشاره می کنند
– C تعداد پیوندهایی است که در صفحه مورد تجزیه و تحلیل قرار می گیرد
– d یک ضریب میرایی است که مربوط به احتمال رها شدن یک صفحه توسط کاربر است (معمولاً 0.85 تنظیم می شود)
هنگامی که صفحات با استناد به صفحات دیگر رای می دهند، رتبه صفحه خود را توزیع می کنند. به عنوان مثال، صفحه A دارای امتیاز PageRank 5 است و به صفحات B و C پیوند می دهد. جدا از سایر پیوندهایی که صفحات B و C ممکن است داشته باشند، صفحات B و C حدود (85%)از امتیاز صفحه، A (4.25) را در مجموع دریافت می کنند. امتیاز (ضرب در ضریب میرایی). اگر صفحه B به صفحه D اشاره کند، امتیاز PageRank D شامل 85٪ امتیاز B و غیره خواهد بود.
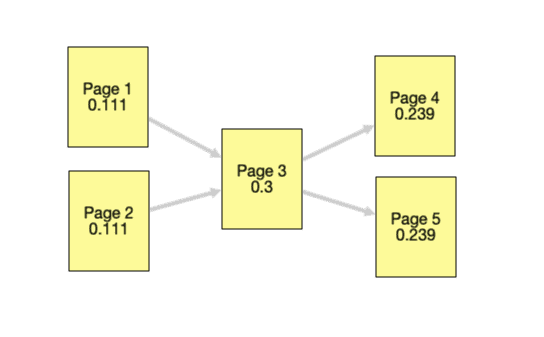
بیایید یک مثال ساده از توزیع رتبه صفحه ساخته شده با شبیه ساز PageRank را بررسی کنیم:
صفحه 3 در اینجا بالاترین امتیاز PageRank را دارد زیرا بیشترین پیوند را به آن دارد. و از آنجایی که صفحه 3 بالاترین امتیاز را دارد، رتبه صفحه ای که در صفحات 4 و 5 کسب می کند نیز بالاتر است.
به طور طبیعی، این محاسبه جدا از یک سناریوی واقعی انجام میشود، با این فرض که فقط این 5 صفحه در وب وجود دارند، اما به روشی ساده نشان میدهد که چگونه مقدار PageRank در بین صفحات وب توزیع میشود.
از آنجایی که PageRank یک معیار معتبر است، توان ارسال شده از طریق پیوندها به صورت سلسله مراتبی محاسبه می شود: یک استناد از یک صفحه رتبه 8 وزن بیشتری از یک نقل قول از یک صفحه رتبه 2 دارد.
اما اگر صفحه شما معمولاً از نقل قول های کمتری استفاده می کند، می تواند از طریق پیوندهایی از صفحاتی که دارای اعتبار کمتر هستند، ارزش صفحه بالاتری کسب کند. به عنوان مثال، صفحه شما از یک منبع PageRank 7 که شامل 10 لینک خروجی است و همچنین از یک منبع PageRank 3 که فقط شامل 3 پیوند است، ارجاع داده می شود.
منبع اول ارزش PageRank 0.105 (0.7 ضربدر ضریب میرایی) را پاس می کند و منبع دوم صفحه شما را 0.15 می کند. با این حال، صفحات با کیفیت بالا و محبوب معمولاً به بسیاری از صفحات دیگر پیوند داده نمیشوند، بنابراین بهتر است همیشه روی دریافت انواع بک لینک از سایتهای قابل اعتماد تمرکز کنید.
2. پیاده روی تصادفی (random walk) در الگوریتم Page Rank
وب را می توان مانند یک نمودار جهت دار نشان داد که در آن گره ها صفحات وب را نشان می دهند و لبه ها پیوندهای بین آنها را تشکیل می دهند. به طور معمول، اگر یک گره (صفحه وب) i به یک گره j مرتبط باشد، به این معنی است که i به j اشاره دارد.
ما باید تعریف کنیم که یک صفحه وب چه اهمیتی دارد. به عنوان اولین رویکرد، می توان گفت که تعداد کل صفحات وب است که به آن اشاره می کنند. اگر به این معیار بسنده کنیم، اهمیت این صفحات وب که به آن اشاره می کنند در نظر گرفته نمی شود.
به عبارت دیگر، یک صفحه وب مهم و یک صفحه وب کم اهمیت وزن یکسانی دارند. رویکرد دیگر این است که فرض کنیم یک صفحه وب اهمیت خود را به طور مساوی در تمام صفحات وب که به آنها پیوند می دهد گسترش می دهد. با انجام این کار، می توانیم امتیاز یک گره j را به صورت زیر تعریف کنیم:
که rᵢ امتیاز گره i و dᵢ درجه خارج آن است
از مثال بالا می توانیم این سیستم خطی را بنویسیم.
با عبور از سمت راست این سیستم خطی به سمت چپ، یک سیستم خطی جدید بدست می آوریم که می توانیم با استفاده از حذف گاوسی آن را حل کنیم. اما این راه حل برای نمودارهای کوچک محدود است. در واقع، از آنجایی که این نوع نمودارها پراکنده هستند و حذف گاوس، ماتریس را در هنگام انجام عملیات آن تغییر می دهد، ما پراکندگی ماتریس را از دست می دهیم و فضای حافظه بیشتری را می گیرد. در بدترین حالت، ماتریس دیگر قابل ذخیره نیست.
3. زنجیره مارکوف از ریاضیات پیج رنک
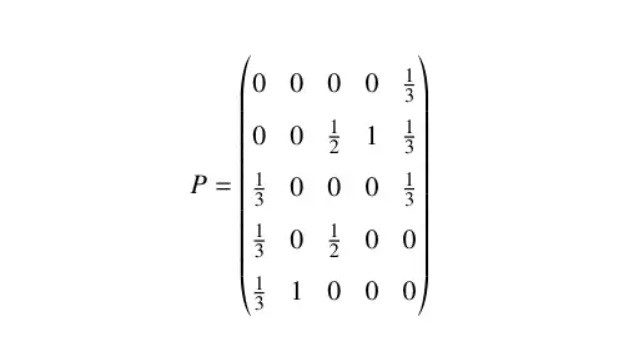
از آنجایی که یک زنجیره مارکوف با یک توزیع اولیه و یک ماتریس انتقال تعریف می شود، نمودار فوق را می توان به عنوان یک زنجیره مارکوف با ماتریس انتقال زیر مشاهده کرد:
ما متوجه شدیم که انتقال P یک ردیف تصادفی است که شرطی برای اعمال قضایای زنجیره مارکوف است.
برای توزیع اولیه، در نظر بگیرید که:
که در آن n تعداد کل گره ها است. این بدان معناست که واکر تصادفی، به صورت تصادفی گره اولیه را انتخاب می کند که از آنجا می تواند به تمام گره های دیگر برسد.
در هر مرحله، واکر تصادفی با توجه به ماتریس انتقال به گره دیگری می پرد. سپس توزیع احتمال برای هر مرحله محاسبه می شود. این توزیع به ما می گوید که واکر تصادفی احتمالاً پس از تعداد معینی از مراحل کجا خواهد بود. توزیع احتمال با استفاده از معادله زیر محاسبه می شود:
توزیع ثابت یک زنجیره مارکوف، توزیع احتمال π با π = Pπ است. این بدان معنی است که توزیع پس از یک مرحله تغییر نخواهد کرد. توجه به این نکته مهم است که همه زنجیره های مارکوف توزیع ثابت را قبول ندارند.
اگر یک زنجیره مارکوف به شدت متصل باشد، به این معنی که هر گره از هر گره دیگری قابل دسترسی است، آنگاه توزیع ثابت را می پذیرد. در مشکل ما هم همینطور است. بنابراین، پس از یک پیاده روی بی نهایت طولانی، می دانیم که توزیع احتمال به توزیع ثابت π همگرا می شود.
تنها کاری که باید انجام دهیم این است که این معادله را حل کنیم:
متوجه شدیم که π یک بردار ویژه از ماتریس P با مقدار ویژه 1 است. به جای محاسبه همه بردارهای ویژه P و انتخاب بردار ویژه با مقدار ویژه 1، از قضیه فروبنیوس-پرون استفاده می کنیم.
طبق قضیه فروبنیوس-پرون، اگر یک ماتریس A یک ماتریس مربع و مثبت باشد (همه ورودی های آن مثبت هستند)، آنگاه دارای مقدار ویژه r مثبت است، مانند |λ| < r، که در آن λ یک مقدار ویژه از A است. بردار ویژه v از A با مقدار ویژه r مثبت است و بردار ویژه مثبت منحصر به فرد است.
در مورد ما، ماتریس P مثبت و مربع است. توزیع ثابت π لزوماً مثبت است زیرا یک توزیع احتمال است. نتیجه می گیریم که π بردار ویژه غالب P با مقدار ویژه غالب 1 است.
برای محاسبه π، از تکرار روش توان استفاده می کنیم که یک روش تکراری برای محاسبه بردار ویژه غالب ماتریس A است. از تقریب اولیه بردار ویژه غالب b که می تواند به طور تصادفی مقداردهی اولیه شود، الگوریتم آن را تا زمان همگرایی با استفاده از الگوریتم زیر:
همانطور که قبلا ذکر شد، توزیع احتمال در زمان t احتمال اینکه واکر بعد از مراحل t در یک گره قرار گیرد را مشخص می کند. یعنی هر چه احتمال بیشتر باشد، گره اهمیت بیشتری دارد. سپس میتوانیم صفحات وب خود را بر اساس توزیع ثابتی که با استفاده از روش توان دریافت میکنیم رتبهبندی کنیم.
4. انتقال از راه دور و عامل میرایی
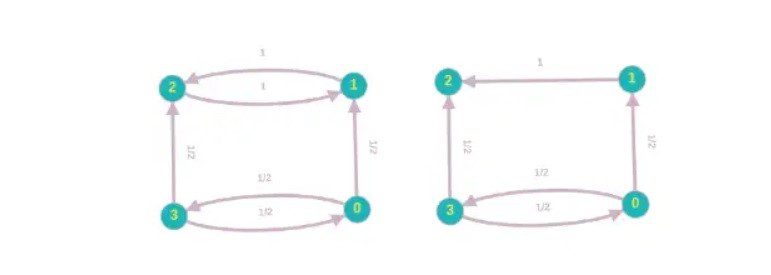
برای مثال، در نمودار وب، میتوانیم یک صفحه وب i را پیدا کنیم که فقط به صفحه وب j و j فقط به i اشاره دارد. این همان چیزی است که ما آن را مشکل تله عنکبوتی می نامیم. ما همچنین می توانیم یک صفحه وب را پیدا کنیم که هیچ لینک خروجی ندارد. معمولاً به آن بن بست می گویند.
در مورد تله عنکبوتی، وقتی واکر تصادفی در مثال بالا به گره 1 می رسد، فقط می تواند به گره 2 بپرد و از گره 2، فقط می تواند به گره 1 و غیره برسد. در مثال بالا، توزیع احتمال به π = (0، 0.5، 0.5، 0) همگرا خواهد شد. این نتیجه مطلوب نیست.
در مورد Dead end ها، وقتی واکر به گره 2 می رسد، نمی تواند به هیچ گره دیگری برسد زیرا هیچ لینک خروجی ندارد. الگوریتم نمی تواند همگرا شود.
برای غلبه بر این دو مشکل، مفهوم دوربری را معرفی می کنیم.
انتقال از راه دور شامل اتصال هر گره از گراف به تمام گره های دیگر است. سپس نمودار کامل خواهد شد. ایده این است که با یک احتمال خاص β، واکر تصادفی با توجه به ماتریس انتقال P به گره دیگری میپرد و با احتمال (1-β)/n، به طور تصادفی به هر گره در نمودار میپرد. سپس ماتریس انتقال جدید R را دریافت می کنیم:
که در آن v بردار یکها و e بردار 1/n است.
β معمولاً به عنوان ضریب میرایی تعریف می شود. در عمل، توصیه می شود β را روی 0.85 تنظیم کنید.
با اعمال دوربری در مثال ما، ماتریس انتقال جدید زیر را دریافت می کنیم:
ماتریس R دارای ویژگی های یکسانی با P است، به این معنی که توزیع ثابت را می پذیرد، بنابراین می توانیم از تمام قضایایی که قبلاً دیدیم استفاده کنیم.
تاثیر الگوریتم پیج رنک در سئو سایت – کمک یا تهدید؟
پیج رنک یکی از عوامل مهمی است که گوگل برای رتبه بندی صفحات وب در نتایج جستجو استفاده می کند. پیج رنک یک امتیاز است که بر اساس تعداد و کیفیت بک لینک های یک صفحه وب محاسبه می شود. صفحاتی که از صفحات معتبرتر لینک می گیرند، خود نیز معتبرتر تلقی می شوند. این به این دلیل است که این صفحات توسط سایر صفحات وب به عنوان منابع ارزشمندی برای اطلاعات شناسایی شده اند. البته، محاسبات این الگوریتم تنها عاملی نیست که گوگل برای رتبه بندی صفحات وب استفاده می کند. عوامل دیگری مانند کیفیت محتوای صفحه، مرتبط بودن صفحه با عبارت جستجو و تجربه کاربری نیز بر رتبه صفحه تأثیر می گذارند؛ با این حال، هنوز هم یکی از عوامل مهمی است که می تواند به بهبود رتبه وب سایت شما در نتایج جستجو کمک کند.
در اینجا چند نکته برای بهبود پیج رنک وب سایت شما آورده شده است:
- محتوای با کیفیت و مرتبط تولید کنید. محتوای با کیفیت و مرتبط به کاربران کمک می کند تا اطلاعات مورد نیاز خود را پیدا کنند. این امر باعث می شود که وب سایت شما توسط سایر صفحات وب به عنوان منبع ارزشمندی برای اطلاعات شناسایی شود.
- بک لینک های معتبر ایجاد کنید. بک لینک های معتبر از سایت هایی ارزش بالا به وب سایت شما می توانند به بهبود پیج رنک شما کمک کنند.
- از ابزارهای سئو استفاده کنید. ابزارهای سئو می توانند به شما کمک کنند تا نقاط قوت و ضعف سئوی وب سایت خود را شناسایی کنید. این امر می تواند به شما کمک کند تا بر روی بهبود عواملی که بر پیج رنک شما تأثیر می گذارند، تمرکز کنید.
با رعایت این نکات می توانید پیج رنک وب سایت خود را بهبود بخشید و رتبه آن را در نتایج جستجو افزایش دهید.
مواردی که در رتبه گرفتن توسط پیج رنک کمک می کند
در اینجا برخی از عواملی که بر امتیاز PageRank یک صفحه وب تأثیر می گذارند آورده شده است:
- تعداد بک لینک ها: هر چه تعداد بک لینک های یک صفحه بیشتر باشد، امتیاز PageRank آن صفحه نیز بیشتر است.
- کیفیت بک لینک ها: بک لینک های معتبرتر امتیاز PageRank بیشتری به یک صفحه می دهند.
- محتوای صفحه: محتوای با کیفیت بالا و مرتبط امتیاز PageRank یک صفحه را افزایش می دهد.
- عمر صفحه: صفحات قدیمی تر معمولاً امتیاز PageRank بالاتری دارند.
اگر به دنبال بهبود رتبه وب سایت خود در نتایج جستجو هستید، می توانید روی بهبود عواملی که بر امتیاز پیج رنک تأثیر می گذارند، تمرکز کنید.
این برای الگوریتم PageRank است. امیدوارم شهود و نظریه پشت الگوریتم PageRank را درک کرده باشید. لطفا نظرات و سوالات خود را با مجموعه ویکی دمی در میان بگذارید.
2 Comments
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.




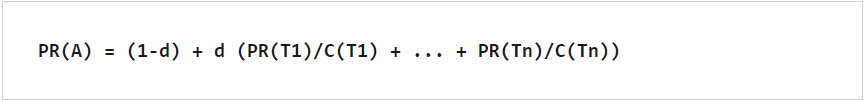




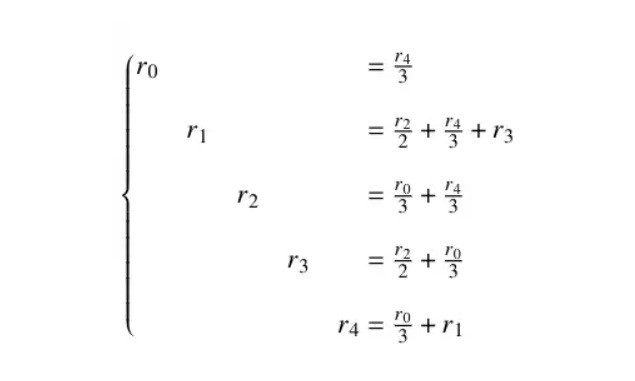


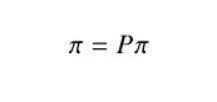


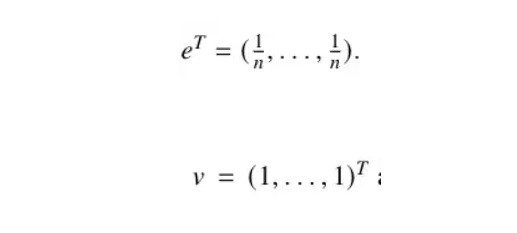
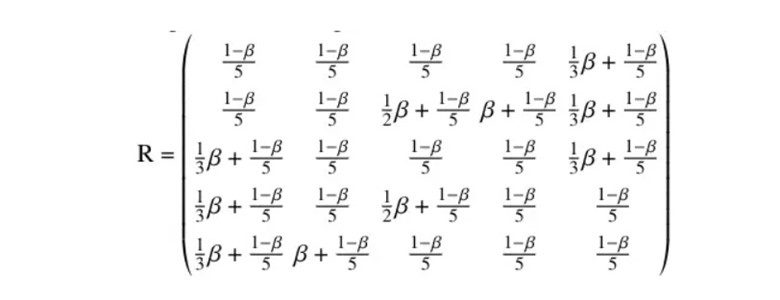
سلام وقت بخیر. سوالم اینه که لینک های نوفالو میگن تو پیج رنک تاثیر نداره. درسته؟
سلام. سمانه جان میگن نمیذاره اما شواهد نشون داد که به مرور زمان تاثیری از خودش به جا میذاره.